2006年 大学入試センター試験 数学ⅠA 解説
第1問〔1〕・〔2〕 第2問 第3問 第4問
第1問〔2〕
(1) 条件 は は がともに有理数であるという条件なので, がともに有理数であるという条件なので,
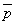 は は のどちらか一方でも有理数ではないというものになる。よって のどちらか一方でも有理数ではないというものになる。よって
「 の少なくとも一方は無理数である」の③になる。 の少なくとも一方は無理数である」の③になる。
(2) 「条件 かつ かつ 」ということは, 」ということは,
 はともに有理数であり,さらに, はともに有理数であり,さらに, は有理数であるというもの。 は有理数であるというもの。
 がともに有理数であれば, がともに有理数であれば, , , はずべて有理数になるので はずべて有理数になるので
必要条件を満たす。
しかし, , , がすべて有理数であっても がすべて有理数であっても がともに有理数とは がともに有理数とは
いえない。
(反証 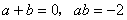 , , のとき, のとき,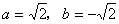 となる) となる)
ということは,十分条件とはいえなくなる。
よって,「必要条件ではあるが十分条件ではない」の①になる。
(3)  ,すなわち, ,すなわち, がともに有理数であれば, がともに有理数であれば, はともに はともに
有理数は真。
 の逆,すなわち, の逆,すなわち, はともに有理数であれば, はともに有理数であれば, がともに がともに
有理数は偽。
 の対偶,すなわち, の対偶,すなわち, はともに有理数はでなければ, はともに有理数はでなければ,
 がともに有理数ではないは真。 がともに有理数ではないは真。
よって,「 」は,「 」は,「 」の逆は偽,「 」の逆は偽,「 」の対偶は 」の対偶は
真となり②。 |


