正弦定理を用いると,
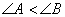 ならば
ならば
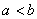 が成り立ちます。
が成り立ちます。
まず,そのことを証明しましょう。
△
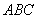 の外接円の半径を
の外接円の半径を
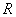 とおくと正弦定理より,
とおくと正弦定理より,
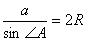 より,
より,
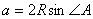
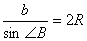 より,
より,
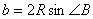
(ⅰ)
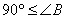 のとき,
のとき,
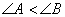 ならば,
ならば,
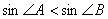 となり,
となり,
 すなわち
すなわち
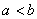 が成り立つ。
が成り立つ。
(ⅱ)
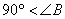 のとき,
のとき,
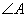 ,
,
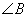 は△
は△
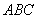 の内角なので,
の内角なので,
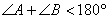 となり,
となり,
 が成り立つ。
が成り立つ。
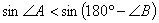 なので,
なので,
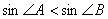 となり,
となり,
 すなわち
すなわち
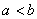 が成り立つ。
が成り立つ。
よって,(ⅰ)(ⅱ)より,いずれの場合でも
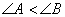 ならば,
ならば,
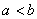 が成り立つ。
が成り立つ。
この証明より,
三角形の辺の大小関係はその対角の大小関係と一致する
ことが分かります。
数学Ⅰの目次へ
数学の目次へ
|


